戻る｜PDFファイルダウンロード

強制振動の微分方程式

　　　　　　　　
を微分演算子を用いて表すことにします。

また、右辺はCos関数ですから、

右辺＝

とおいて

実数部を解とすればかまいません。したがって、
　　　　　　　

とすることができます。公式から

　　　　　　　　　

が成立しますので、
　　　　　　

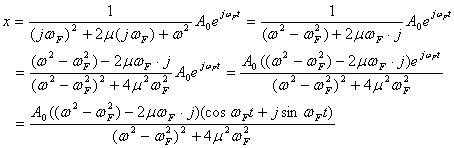
となります。右辺は、Cos関数ので、実数部だけをとると、

　　　　　　

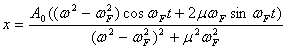
ここで、
　　　　　　

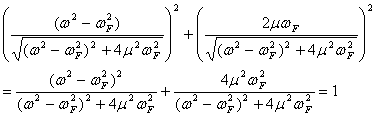
であることに着目すると、

　　　　　　

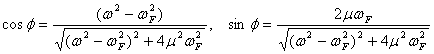
となる変数φを導入して、

　　　　　　
　　　　　　
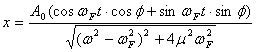
と表現することができます。三角関数の加法定理から、解は、

　　　　　　　　

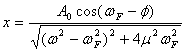
となります。この式を解釈すると、系の振動の角振動数は、

与えられた強制振動

と同じ振動数で、位相が

だけずれた振動となります。

また、振幅
　　　　　　

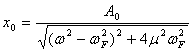
は角振動数で変化します。上式の分母の根号の中は、

　　　　　

となりますので、これを

で微分すると

すなわち、

のとき0となり、極小値となります。

ただし、

のとき振動していないことを示します。なお、

あるいは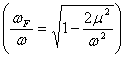

のとき、振幅が最大となります。これを共振角振動数といいます。

この式を振幅の式に代入すると、

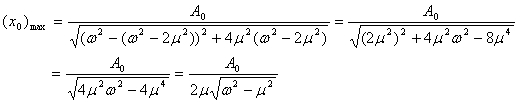
なります。

のとき、

による振幅変化をグラフ化すると

以下のようになります。